Predictive Modeling

Data Literacy

Daniel Winkler

Institute for Retailing & Data Science

Predictive modeling

  • Not concerned with causal relationship
    • causal model typically worse in terms of prediction
  • Allows flexible model structure
  • Goal: extrapolate well (small error) to unknown outcome given new observed input
  • Definition of “error” (loss) depends on the outcome variable and problem
    (e.g., binary \(\rightarrow\) sensitivity/specificity, continuous \(\rightarrow\) squared/absolute error)
  • Fundamental issue: overfitting
    • Each observed outcome contains signal and noise
    • signal: part that is associated with inputs
    • noise: additional variation e.g., measurement error, unobserved factors, random nature of outcome
      • will be different in new data
    • overfitting: in addition to the signal the model also picks up on the noise of the data used to “fit” (train) the parameters

Bias-variance tradeoff

source

A first example

library(modelsummary)
library(Metrics)

set.seed(42)
x <- runif(1000, -100, 100)
y <- 12.5 + 7 * x + rnorm(
    length(x), mean = 0, sd = 1000
    )
model_data <- data.frame(x,y)
mod.ols <- lm(y~x, data = model_data)
modelsummary(list(OLS = mod.ols), output="markdown")
OLS
(Intercept) -17.447
(31.640)
x 7.676
(0.543)
Num.Obs. 1000
R2 0.167
R2 Adj. 0.166
AIC 16656.8
BIC 16671.6
Log.Lik. -8325.414
F 200.071
RMSE 998.72

Check for overfitting: data prep

  • Train/Test split
    • Use e.g., 80% of the sample to fit the model and 20% to test its performance on new data
  • In real life: do this many times with different splits to see patterns
library(rsample)
split_xy <- initial_split(model_data, prop = 0.8)
training_xy <- training(split_xy)
testing_xy <- testing(split_xy)
print("Signal vs. Noise")
[1] "Signal vs. Noise"
summary(training_xy)
       x                 y           
 Min.   :-99.919   Min.   :-3495.10  
 1st Qu.:-53.554   1st Qu.: -786.51  
 Median : -3.720   Median :  -60.38  
 Mean   : -1.075   Mean   :  -49.86  
 3rd Qu.: 51.472   3rd Qu.:  722.85  
 Max.   : 99.698   Max.   : 3155.77  
summary(testing_xy)
       x                 y           
 Min.   :-99.952   Min.   :-3410.78  
 1st Qu.:-55.411   1st Qu.: -546.54  
 Median : -5.878   Median :   58.90  
 Mean   : -7.446   Mean   :   22.05  
 3rd Qu.: 42.628   3rd Qu.:  702.45  
 Max.   : 98.159   Max.   : 3910.81

Check for overfitting

  • Check for differences in model performance in the training and test samples
  • RMSE: Root Mean Squared Error \(\sqrt{\frac{1}{n}\sum_{i=1}^n (y - \hat y)^2}\) 
mod.ols.train <- lm(y ~ x, data =  training_xy)
modelsummary(mod.ols.train, gof_omit = "R2|IC|Log|F")
 (1)
(Intercept) −41.424
(35.892)
x 7.849
(0.612)
Num.Obs. 800
RMSE 1013.74 
Metrics::rmse(training_xy$y, predict(mod.ols.train))
[1] 1013.745
Metrics::rmse(testing_xy$y, predict(mod.ols.train, testing_xy))
[1] 938.0764

Check for overfitting: \(k\)-fold Cross-Validation

  • Shuffle the data
    • Very flexible models may learn the data ordering
  • Create \(k\) equally sized non-overlapping test splits
  • run the model \(k\) times using a different split as the test set in each run
  • Size of each split \(n/k\)

source

Let’s overfit

  • Model that includes 25 powers of x (de-correlated)
  • Now RMSE is worse in the test set: the model learned noise of the training data
mod.powers.train <- lm(y ~ poly(x, degrees = 25), data =  training_xy)

Metrics::rmse(training_xy$y, predict(mod.powers.train))
[1] 987.8615
Metrics::rmse(testing_xy$y, predict(mod.powers.train, testing_xy))
[1] 1002.229

Real example: Gradient boosting

XGBoost

  • Flexible non-parametric model
  • Regularization (i.e., shrinkage) of parameters -> variable selection
  • Regularization of model -> prevent overfitting
  • Scalable algorithm

source

Avoid Overfitting

  • Which paramters does the model have that “restrict” the training?
  • Problem:
    • Too restrictive: underfitting
    • Too flexible: overfitting
  • Tune parameters to find the reasonable middle

source

Model setup

library(tidymodels)
library(palmerpenguins)
mod.boost <- boost_tree(
    mode   = "classification",
    engine = "xgboost",
    learn_rate = tune()
)
mod.boost
Boosted Tree Model Specification (classification)

Main Arguments:
  learn_rate = tune()

Computational engine: xgboost

Hyperparamter tuning setup

  • Run the model multiple times using different values for the learning rate
  • Select the one that performs best
set.seed(1)
random_lr <- grid_random(
    extract_parameter_set_dials(mod.boost), 
    size = 10)
random_lr
# A tibble: 10 × 1
   learn_rate
        <dbl>
 1    0.00461
 2    0.00852
 3    0.0270 
 4    0.186  
 5    0.00319
 6    0.176  
 7    0.230  
 8    0.0449 
 9    0.0374 
10    0.00143

Data setup

  • Predict the penguin species based on the observed data
  • Numeric features can be used as they are
  • Categorical features have to be encoded into numeric features
    • most common: one-hot encoding (indicator function)
    • in this case: island, sex 
penguins <- drop_na(penguins)
penguin_dummies <- recipe(species ~ ., penguins) |>
    step_dummy(all_nominal_predictors(), one_hot = TRUE)
# see ?step_dummy for other encoding options
head(penguins)
# A tibble: 6 × 8
  species island    bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
  <fct>   <fct>              <dbl>         <dbl>             <int>       <int>
1 Adelie  Torgersen           39.1          18.7               181        3750
2 Adelie  Torgersen           39.5          17.4               186        3800
3 Adelie  Torgersen           40.3          18                 195        3250
4 Adelie  Torgersen           36.7          19.3               193        3450
5 Adelie  Torgersen           39.3          20.6               190        3650
6 Adelie  Torgersen           38.9          17.8               181        3625
# ℹ 2 more variables: sex <fct>, year <int>

Putting the setup together

  • Create a workflow that combines model and data preprocessing
  • Set up \(k\)-fold cross-validation
    • Here \(v\)-fold for whatever reason but just think \(k = v\)
  • Tune the learning rate
## Model & data preparation
species_pred_wf <- workflow() |>
    add_model(mod.boost) |>
    add_recipe(penguin_dummies)
## Cross-validation
specied_pred_cv <- vfold_cv(penguins, v = 5)
## Learning rate tuning
lr_tuning <- tune_grid(
    species_pred_wf,
    resamples = specied_pred_cv,
    grid = random_lr,
    metrics = metric_set(bal_accuracy),
    control = control_grid(verbose = FALSE)
)
lr_tuning
# Tuning results
# 5-fold cross-validation 
# A tibble: 5 × 4
  splits           id    .metrics          .notes          
  <list>           <chr> <list>            <list>          
1 <split [266/67]> Fold1 <tibble [10 × 5]> <tibble [0 × 3]>
2 <split [266/67]> Fold2 <tibble [10 × 5]> <tibble [0 × 3]>
3 <split [266/67]> Fold3 <tibble [10 × 5]> <tibble [0 × 3]>
4 <split [267/66]> Fold4 <tibble [10 × 5]> <tibble [0 × 3]>
5 <split [267/66]> Fold5 <tibble [10 × 5]> <tibble [0 × 3]>

Choosing the best parameter value

  • Combine the metrics from all CV runs
  • Select the learning rate to use for model training
  • Update the model & workflow
lr_tuning |>
    collect_metrics() |>
    arrange(-mean) |>
    select(learn_rate, mean, std_err)
# A tibble: 10 × 3
   learn_rate  mean std_err
        <dbl> <dbl>   <dbl>
 1    0.186   0.989 0.00420
 2    0.176   0.989 0.00420
 3    0.230   0.989 0.00420
 4    0.0449  0.986 0.00510
 5    0.00461 0.983 0.00504
 6    0.00852 0.983 0.00504
 7    0.00319 0.983 0.00504
 8    0.00143 0.983 0.00504
 9    0.0270  0.980 0.00494
10    0.0374  0.980 0.00494
## Select best learning rate
best_lr <- lr_tuning |> select_best()
## Set best learning rate for the model
species_pred_wf_best1 <- species_pred_wf |>
    finalize_workflow(best_lr)
species_pred_wf_best1
══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: boost_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
1 Recipe Step

• step_dummy()

── Model ───────────────────────────────────────────────────────────────────────
Boosted Tree Model Specification (classification)

Main Arguments:
  learn_rate = 0.186431577754487

Computational engine: xgboost

Fit the final model

  • Fit the model and add predictions to the original data
  • Plot the confusion matrix (true vs. predicted class counts)
library(colorspace)
set.seed(1)
penguin_fit <- species_pred_wf_best1 |>
    fit(penguins) 
penguins$pred <- penguin_fit |>
    predict(penguins) |>
    pull(.pred_class)
penguins |>
    mutate(pred = as.factor(pred)) |>
    conf_mat(species, pred) |>
    autoplot(type = 'heatmap') +
    scale_fill_continuous_diverging("Purple-Green")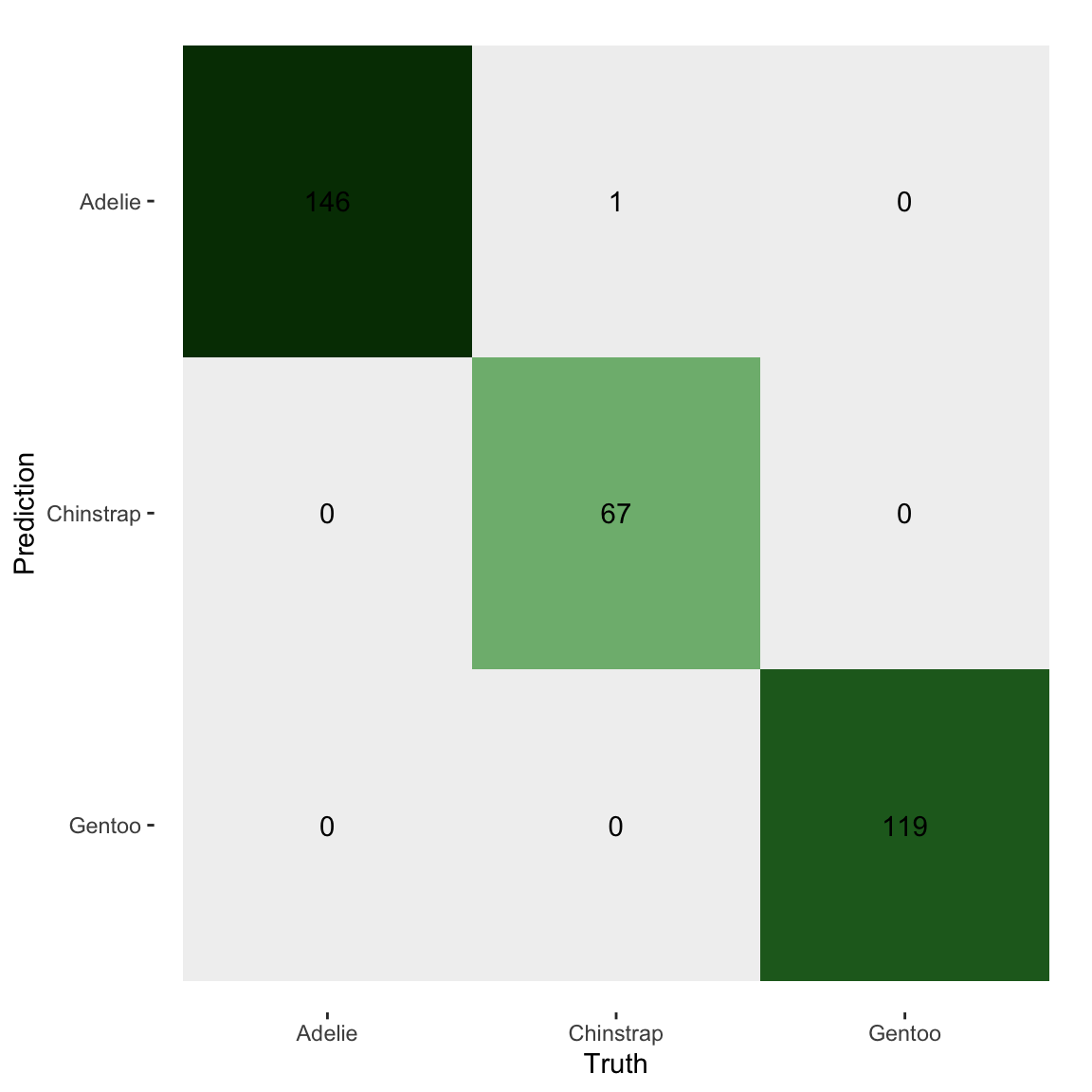

Determine variable importance

Code
penguin_fit |>
    extract_fit_parsnip() |>
    vip::vip(include_type=TRUE, type = 'gain') +
    theme_classic() +
    theme(
        axis.text = element_text(size=25),
        axis.title = element_text(size=25))

Exercise

Avoid overfitting

  • In the previous example the same data was used for training and prediction
  • Implement a strategy to show that we are not overfitting
  • Hint: read the Details section of ?initial_split

Solution

Code
set.seed(1)
penguin_split <- initial_split(penguins, strata = species)
ptrain <- training(penguin_split)
ptest <- testing(penguin_split)
set.seed(1)
ptest$pred <- species_pred_wf_best1 |>
    fit(ptrain) |>
    predict(ptest) |>
    pull(.pred_class)
ptest |>
    bal_accuracy(species, pred)
# A tibble: 1 × 3
  .metric      .estimator .estimate
  <chr>        <chr>          <dbl>
1 bal_accuracy macro          0.987
Code
ptest |>
    mutate(pred = as.factor(pred)) |>
    conf_mat(species, pred) |>
    autoplot(type = 'heatmap') +
    scale_fill_continuous_diverging("Purple-Green")

Alternative Solution

  • last_fit fits on the training split and evaluates on the test split
Code
set.seed(1)
final_fit <- species_pred_wf_best1 |>
    last_fit(
        penguin_split, 
        metrics = metric_set(bal_accuracy))
final_fit |> 
    collect_metrics()
# A tibble: 1 × 4
  .metric      .estimator .estimate .config             
  <chr>        <chr>          <dbl> <chr>               
1 bal_accuracy macro          0.987 Preprocessor1_Model1

Data Literacy