B-DiDi a Dynamic Bayesian approach to DiD

Marketing Science Conference 2024

Daniel Winkler

WU-Vienna

Pascal Güntürkün

WU-Vienna

Peter Knaus

Harvard University

June 27, 2024

Overview

3 Parts

  1. Motivation: “Why opt-out defaults save fewer lives than we think”
  2. Dynamic Bayesian Approach to DiD
    1. Proposed model
    2. Simulation results
  3. Application to policy changes

Motivation: Why opt-out defaults save fewer lives than we think

with Pascal Güntürkün (WU Vienna), Sinika Studte (HSBA Hamburg School of Business Administration), Michel Clement (University of Hamburg), Eva-Maria Merz (VU Amsterdam; Sanquin Research), Elisabeth Huis in ’t Veld (Tilburg University), Jonathan Tan (Nanyang Technical University), Eamonn Ferguson (The University of Nottingham; Cambridge University)

Exploiting changes in policy nudges

  • Promote socially desirable behavior through subtle changes in the choice environment
  • While freedom of choice remains in tact
  • Popular with policy makers and researchers
  • Most popular: Opt-out default
    • Consent to socially desireable behavior presumed
    • Individuals can freely opt-out
    • Examples: organ donation, retirement savings, green energy usage
  • We studied opt-in vs. opt-out defaults for deceased organ donation

What effect do you expect?

Can default nudges backfire?

  • Consensus based on meta-analyses: opt-out default policies have positive effects on targeted behavior
    • e.g., Benartzi et al., 2017; Jachimowicz et al., 2019; Mertens et al., 2022; Steffel et al., 2019
  • How does substitutive behavior to reach the same goal change?
    • Living vs. deceased organ donation,
    • energy usage reduction vs. green energy usage,
    • masks vs. vaccine

Switching to opt-out organ donation

  • Not enough organs available
  • Deceased donations increase
  • Living organ donations???

Evaluating the policy change: quasi-experimental setting

Difference-in-differences basics

  • Number of available organs observed
    • for two countries
    • over two periods
  • Country A switches to opt-out between period 1 and 2
  • Country B remains opt-in
  • The change (difference B) in country B is used as the counterfactual for the change (difference A) in country A
  • Estimator: difference in differences B and A

DiD basics

  • Key assumption: number of available organs would have developed in parallel without the switch

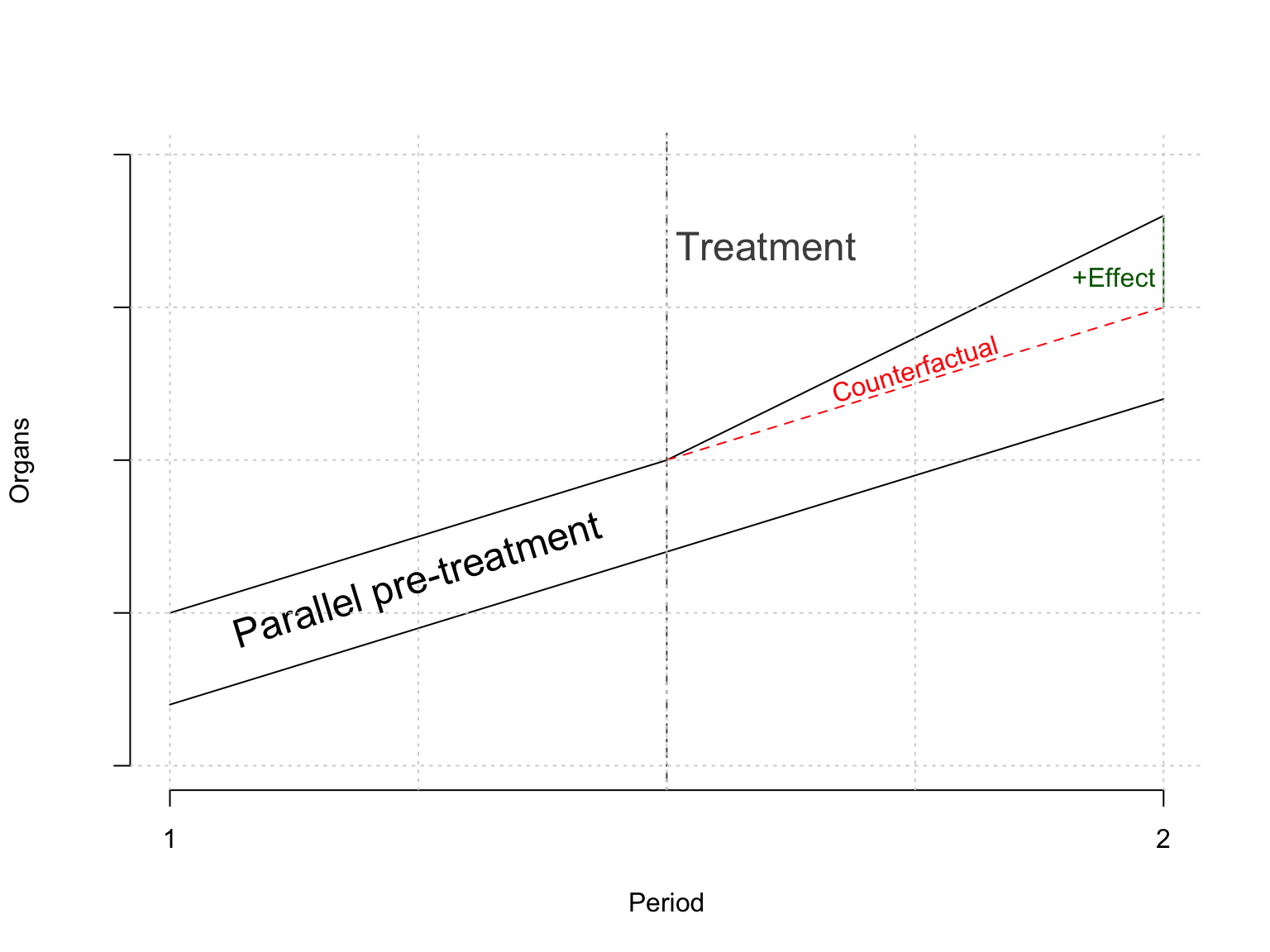
Method: Callaway and Sant’Anna (2021)

  • For countries adopting the switch at different times
  • Select units that are not (yet) treated as controls
  • Estimate group-time average treatment effect & aggregate

Research problem

  • Not suitable for inference on small treated groups (<5)
  • Frequentist methods not suitable to show null effect and parallel trends (Wasserstein, Schirm, and Lazar 2019)
    • Bayesian shrinkage prior lets data decide if an effect is present
    • Savage-Dickey density ratios / ROPE can be used to show null effect (Wagenmakers et al. 2010)
  • High variance

Solution: B-DiDi

For each group \(g\) estimate two models:

  • Pre-treatment model to gain confidence in parallel trends
  • Post-treatment model to estimate treatment effects

General setup

  • Use time-varying parameters
    • Assumption: trend-violations/treatment effects evolve smoothly
    • “A treatment effect today makes a similar effect likely tomorrow.”
  • Poentially correct treatment effect using the estimate of trend violations (in the pre-period) similar to Rambachan and Roth (2023)

Estimation

  • Gaussian RW State Space model (Cadonna, Frühwirth-Schnatter, and Knaus 2020) \[ \begin{aligned} \beta_{g,t} &= \beta_{g,t-1} + w_{g,t}, \quad w_{g,t} \sim N_4(\mathbf{0}, \mathbf{Q_{g}}) \\ y_{g,t} &= X_{g,t} \beta_{g,t} + \epsilon_{g,t}, \quad \epsilon_{g,t} \sim N_p(\mathbf{0}, Diag(\sigma^2_g)) \\ \mathbf{Q_g} &= Diag(\theta_{1,g}, \dots, \theta_{4,g}) \end{aligned} \]

  • Non-centered paramterization (Frühwirth-Schnatter and Wagner 2010)

\[ \begin{aligned} \tilde{\beta}_{g,t} &= \tilde{\beta}_{g,t-1} + \tilde{w}_{g,t}, \quad \tilde{w}_{g,t} \sim N_4(\mathbf{0}, \mathbf{I})\\ y_{g,t} &= X_{g,t} \beta_g + X_{g,t} Diag(\sqrt{\theta_{g, 1}}, \dots, \sqrt{\theta_{g,4}}) \tilde \beta_{g,t} + \epsilon_{g,t}, \quad \epsilon_{g,t} \sim N_p(0, Diag(\sigma^2_g)) \end{aligned} \]

  • Diffuse Normal, inverse gamma prior for pre-treatment model

Post-treatment model

Tripple Gamma (Cadonna, Frühwirth-Schnatter, and Knaus 2020) priors for \(\sqrt{\theta_{g,j}}\) and \(\beta_{g,j}\)1

\[ \sqrt{\theta}_j\left|\xi_j^2 \sim N\left(0, \xi_j^2\right),\\ \xi_j^2\right| a^{\xi}, \kappa_j^2 \sim G\left(a^{\xi}, \frac{a^{\xi} \kappa_j^2}{2}\right),\\ \kappa_j^2 \mid c^{\xi}, \kappa_B^2 \sim G \left(c^{\xi}, \frac{c^{\xi}}{\kappa_B^2}\right) \]

\[ \beta_j\left|\phi_j^2 \sim N\left(0, \phi_j^2\right), \\ \phi_j^2\right| a^\phi, \lambda_j^2 \sim G\left(a^\phi, \frac{a^\phi \lambda_j^2}{2}\right), \\ \lambda_j^2 \mid c^\phi, \lambda_B^2 \sim G\left(c^\phi, \frac{c^\phi}{\lambda_B^2}\right) \]

Post-treatment model

Global shrinkage (\(\lambda_B^2,\ \kappa_B^2\)) also as in (Cadonna, Frühwirth-Schnatter, and Knaus 2020) s.t.

  • \(\frac{\lambda_B^2}{2} \sim F(2a^\lambda, 2c^\lambda)\) and
  • \(\frac{\kappa_B^2}{2} \sim F(2a^\kappa, 2c^\kappa)\)

Does it work?

DGP: No trend violation, no treatment effect

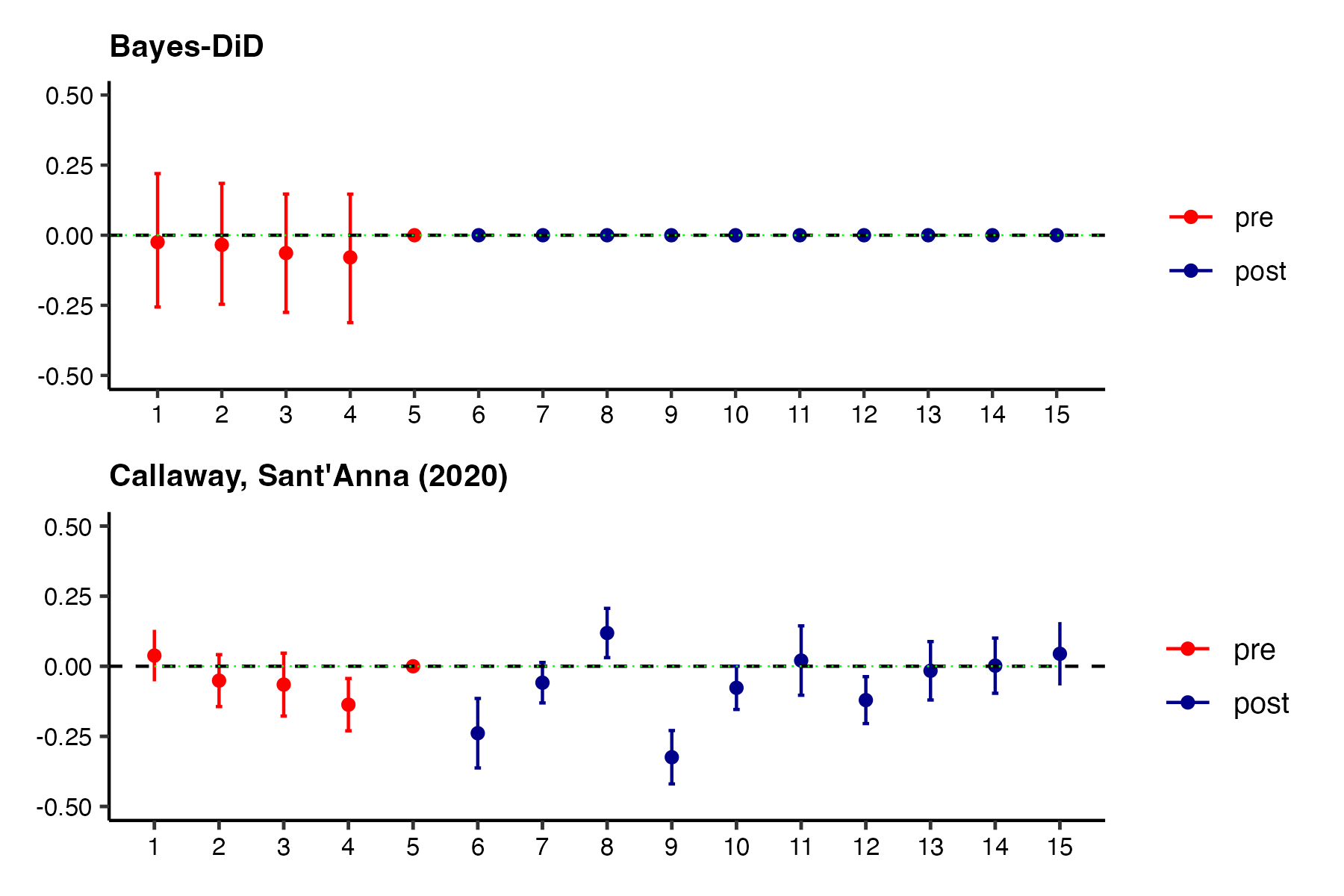
DGP: No trend violation, constant effect

DGP: No trend violation, increasing effect

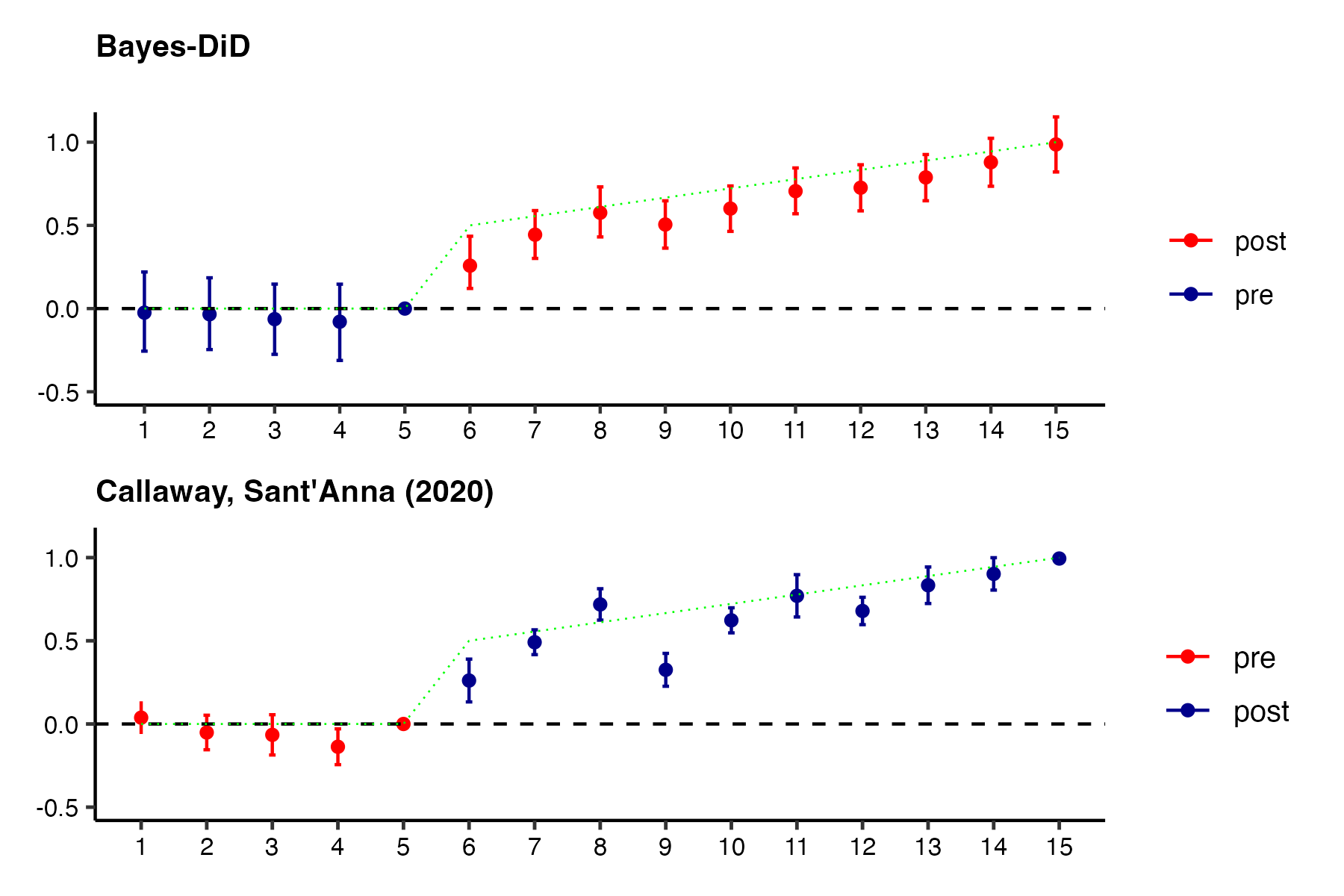
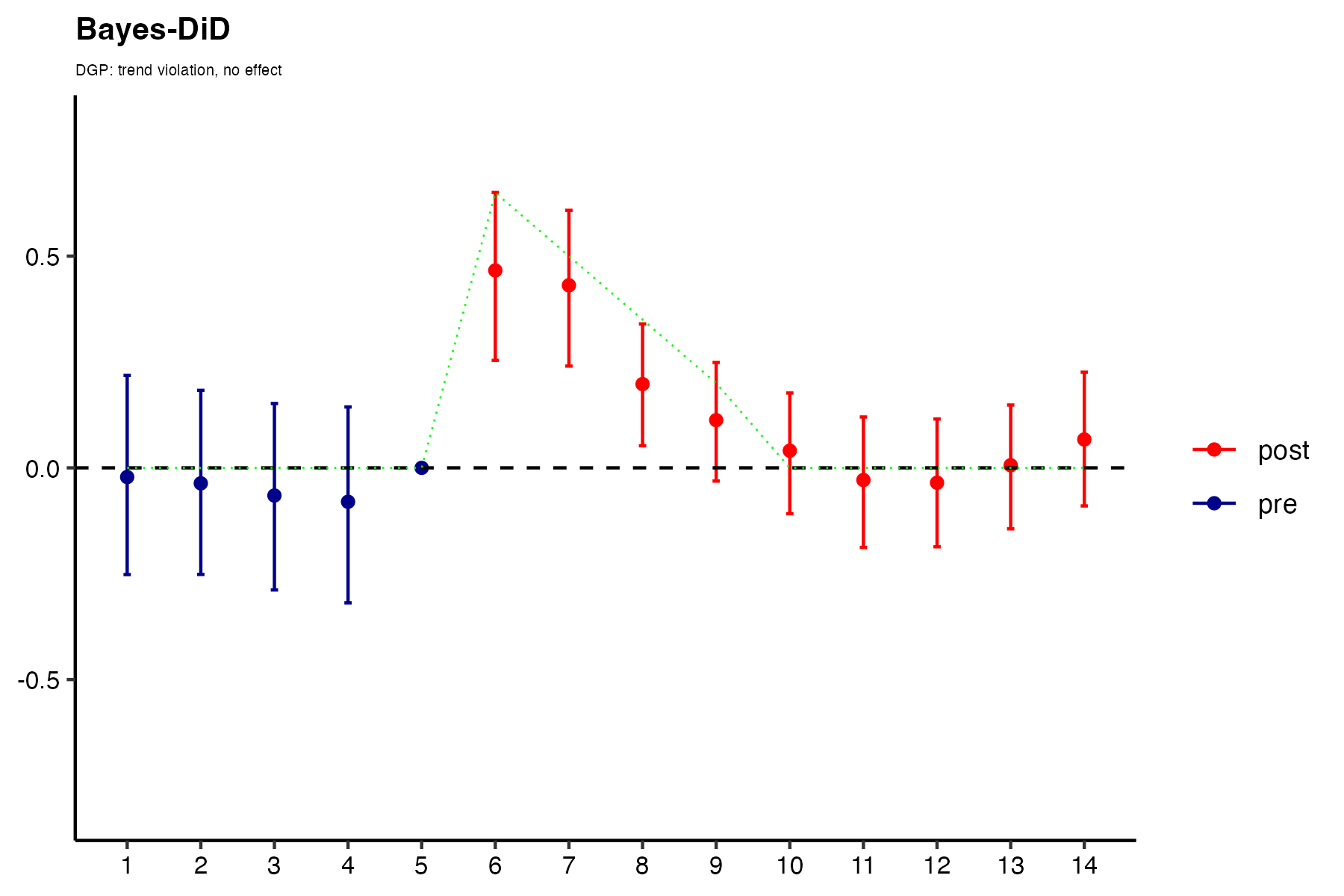
DGP: Trend violation, no effect

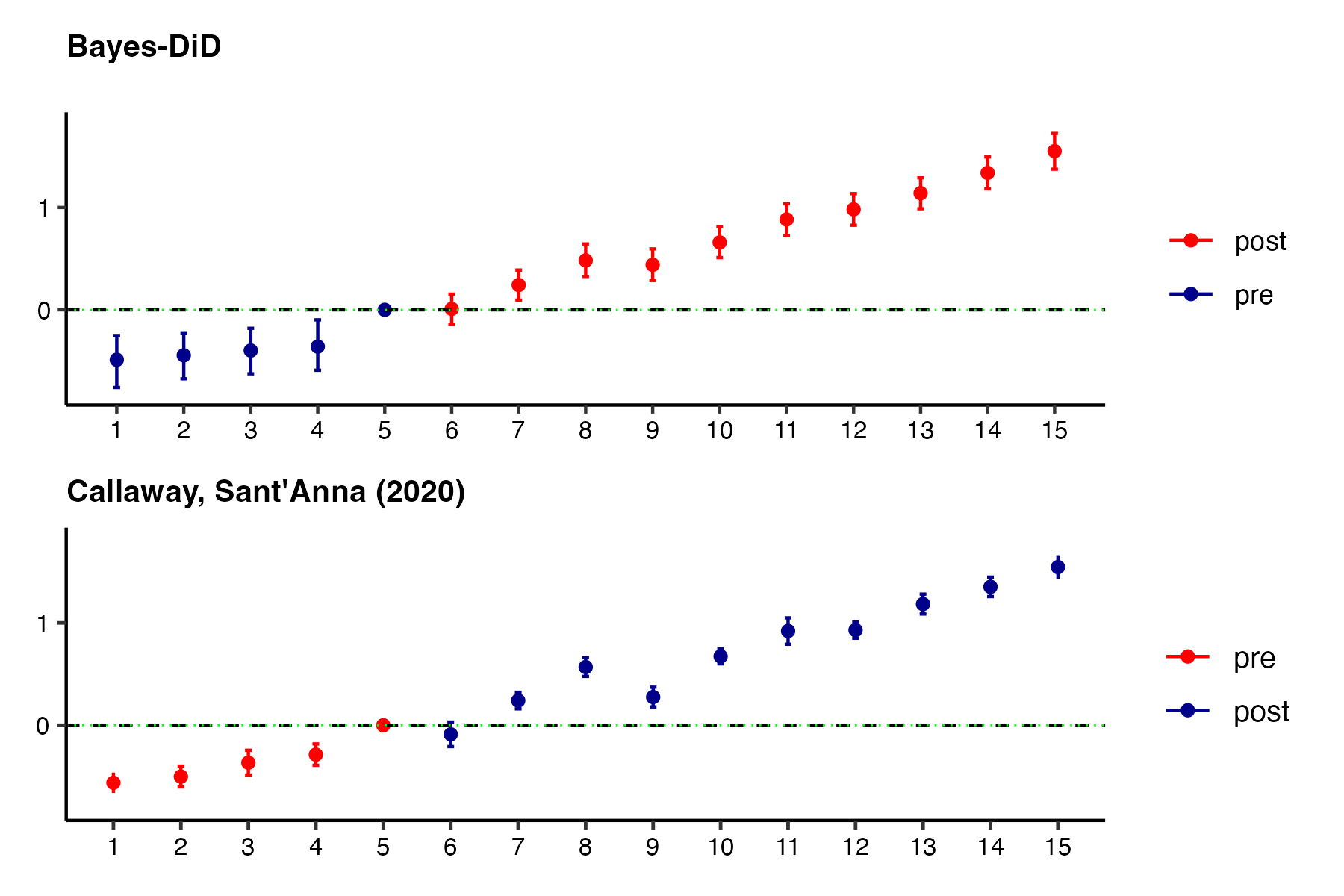
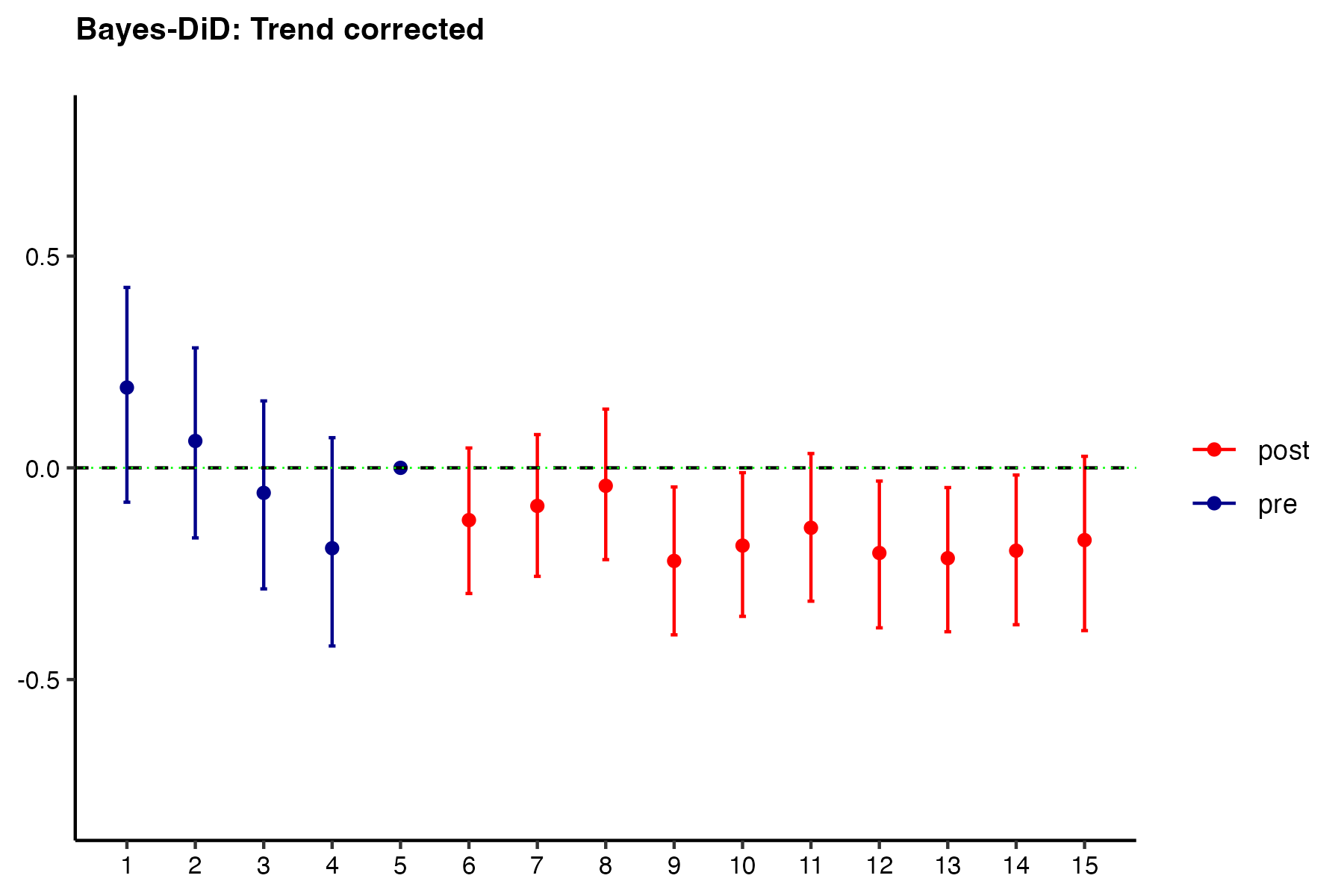
Correcting trend violations

Corrected by implied violation based on posterior-median of pre-treatment model (similar to Rambachan and Roth 2023)

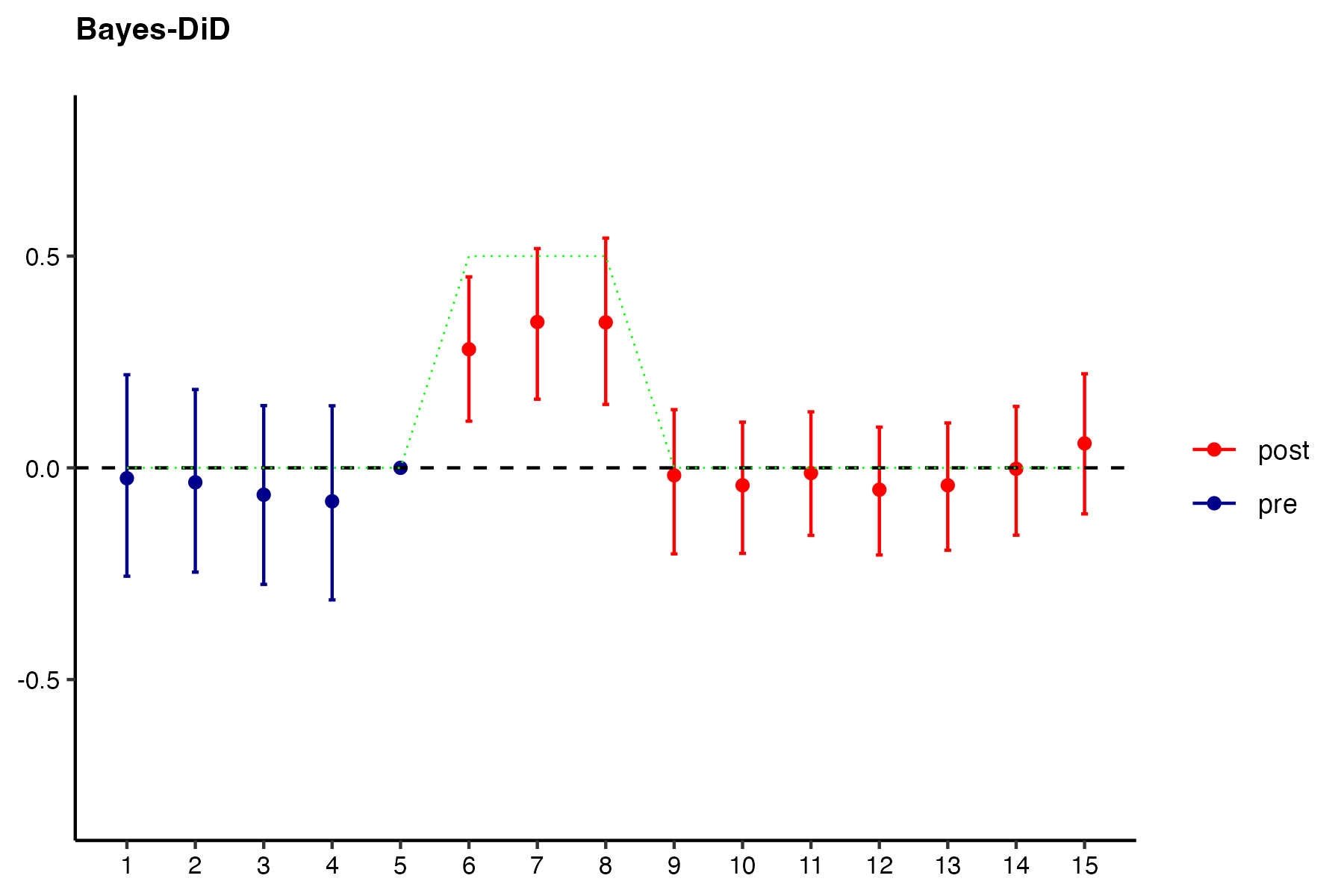
Three periods of effects

Declining effect with bottom-out

Application to organ donation policy

Wales: a success story

Wales: pre-trend corrected

Wales: Aggregate effect

Slovakia: negative effect on living donations

Slovakia: null effect of policy change

Summary & Outlook

  • B-DiDi will be published as a Julia package
  • Parameters are learned across time to use the data efficiently
  • Performs very well when there are few treated units (even just 1!)
  • Triple-Gamma is a flexible shrinkage prior for determining whether an effect is non-zero
    • Has properties of Bayesian model averaging (accounts for model uncertainty)
    • Nests many popular shrinkage priors (e.g., Lasso, Horseshoe)
  • Having the Bayesian posterior for the treatment effect can provide evidence for null-effect
    • Savage-Dickery ratio, Region Of Practical Equivalence

Thank you for your attention

Any questions?

Appendix

Triple-Gamma marginal prior

Treatment effect

  • \(Y_{i,t}\) … outcome of unit \(i\) at time \(t\)

Potential outcomes (Rubin 2005)

  • \(Y_{i,t}(0)\) … \(Y_{i,t}\) given \(i\) is not treated at \(t\)
  • \(Y_{i,t}(1)\) … \(Y_{i,t}\) give \(i\) is treated at \(t\)
  • Observed: \(Y_{i,t} = \mathbb{1}(treated_{i,t}) Y_{i,t}(1) + \left[1 - \mathbb{1}(treated_{i,t})\right] Y_{i,t}(0)\)
  • Individual treatment effect: \(\tau_{i,t} = Y_{i,t}(1) - Y_{i,t}(0)\)

Treatment effect

  • \(Y_{i,t}\) … outcome of unit \(i\) at time \(t\)

Potential outcomes (Rubin 2005)

  • \(Y_{i,t}(0)\) … \(Y_{i,t}\) given \(i\) is not treated at \(t\)
  • \(Y_{i,t}(1)\) … \(Y_{i,t}\) give \(i\) is treated at \(t\)
  • Observed: \(Y_{i,t} = \mathbb{1}(treated_{i,t}) Y_{i,t}(1) + \left[1 - \mathbb{1}(treated_{i,t})\right] Y_{i,t}(0)\)
  • Individual treatment effect: \(\tau_{i,t} = Y_{i,t}(1) - Y_{i,t}(0)\)
Group t = 1 t = 2
\(g = 2\) \(Y_{i,1}(0)\) \(Y_{i, 2}(1)\)
\(g = \infty\) \(Y_{j,1}(0)\) \(Y_{j, 2}(0)\)

Average Treatment Effect on the Treated (\(\tau_{g=2}\))

  • \(\bar Y_{g=k, t}\)… average outcome of group \(k\) at time \(t\)
  • \(\delta_{g=\cdot}\)… trend of the outcome for \(g = \cdot\)
  • \(\delta_{g=\cdot} = \delta\) for \(g = 2\) and \(g = \infty\) under parallel trends

\[ \begin{aligned} \bar Y_{g=2, 2} - \bar Y_{g=2, 1} &= \delta_{g=2} + \tau_{g=2} \\ \bar Y_{g=2, 2} - \bar Y_{g=2, 1} &= \bar Y_{g=\infty, 2} - \bar Y_{g=\infty, 1} + \tau_{g=2} \\ \left[\bar Y_{g=2, 2} - \bar Y_{g=2, 1}\right] - \left[\bar Y_{g=\infty, 2} - \bar Y_{g=\infty, 1}\right] &= \tau_{g=2} \end{aligned} \]

References

Cadonna, Annalisa, Sylvia Frühwirth-Schnatter, and Peter Knaus. 2020. “Triple the Gamma&mdash;a Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models.” Econometrics 8 (2): 20. https://doi.org/10.3390/econometrics8020020.
Callaway, Brantly, and Pedro H. C. Sant’Anna. 2021. “Difference-in-Differences with Multiple Time Periods.” Journal of Econometrics, Themed issue: Treatment effect 1, 225 (2): 200–230. https://doi.org/10.1016/j.jeconom.2020.12.001.
Frühwirth-Schnatter, Sylvia, and Helga Wagner. 2010. “Stochastic Model Specification Search for Gaussian and Partial Non-Gaussian State Space Models.” Journal of Econometrics 154 (1): 85–100. https://doi.org/10.1016/j.jeconom.2009.07.003.
Knaus, Peter, and Sylvia Frühwirth-Schnatter. 2023. “The Dynamic Triple Gamma Prior as a Shrinkage Process Prior for Time-Varying Parameter Models.” arXiv. https://doi.org/10.48550/arXiv.2312.10487.
Rambachan, Ashesh, and Jonathan Roth. 2023. “A More Credible Approach to Parallel Trends.” Review of Economic Studies 90 (5): 2555–91. https://doi.org/10.1093/restud/rdad018.
Rubin, Donald B. 2005. “Causal Inference Using Potential Outcomes: Design, Modeling, Decisions.” Journal of the American Statistical Association 100 (469): 322–31. https://www.jstor.org/stable/27590541.
Wagenmakers, Eric-Jan, Tom Lodewyckx, Himanshu Kuriyal, and Raoul Grasman. 2010. “Bayesian Hypothesis Testing for Psychologists: A Tutorial on the Savage–Dickey Method.” Cognitive Psychology 60 (3): 158–89. https://doi.org/10.1016/j.cogpsych.2009.12.001.
Wasserstein, Ronald L., Allen L. Schirm, and Nicole A. Lazar. 2019. “Moving to a World Beyond ‘p < 0.05’.” The American Statistician 73 (March): 1–19. https://doi.org/10.1080/00031305.2019.1583913.